结合 Guava 源码解读布隆过滤器

发表于 更新于 分类于 阅读次数：

BloomFilter（布隆过滤器）是一种可以高效地判断元素是否在某个集合中的算法。

在很多日常场景中，都大量存在着布隆过滤器的应用。例如：检查单词是否拼写正确、网络爬虫的 URL 去重、黑名单检验，微博中昵称不能重复的检测等。

在工业界中，Google 著名的分布式数据库 BigTable 也用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的 IO 次数；Google Chrome 浏览器使用 BloomFilter 来判断一个网站是否为恶意网站。

对于以上场景，可能很多人会说，用 HashSet 甚至简单的链表、数组做存储，然后判断是否存在不就可以了吗？

当然，对于少量数据来说，HashSet 是很好的选择。但是对于海量数据来说，BloomFilter 相比于其他数据结构在空间效率和时间效率方面都有着明显的优势。

但是，布隆过滤器具有一定的误判率，有可能会将本不存在的元素判定为存在。因此，对于那些需要 “零错误” 的应用场景，布隆过滤器将不太适用。具体的原因将会在第二部分中介绍。

同时其他章节的安排如下：

  • 在本文的第二部分，本文将会介绍 BloomFilter 的基本算法思想；
  • 第三部分将会基于 Google 开源库 Guava 来讲解 BloomFilter 的具体实现；
  • 在第四部分中，将会介绍一些开源的 BloomFilter 的扩展，以解决目前 BloomFilter 的不足。

算法讲述

布隆过滤器是基于 Hash 来实现的，在学习 BloomFilter 之前，也需要对 Hash 的原理有基本的了解。个人认为，BloomFilter 的总体思想实际上和 bitmap 很像，但是比 bitmap 更节省空间，误判率也更低。

BloomFilter 的整体思想并不复杂，主要是使用 k 个 Hash 函数将元素映射到位向量的 k 个位置上面，并将这 k 个位置全部置为 1。当查找某元素是否存在时，查找该元素所对应的 k 位是否全部为 1 即可说明该元素是否存在。

算法流程

BloomFilter 的整体算法流程可总结为如下步骤：

  1. BloomFilter 初始化为 m 位长度的位向量，每一位均初始化为 0
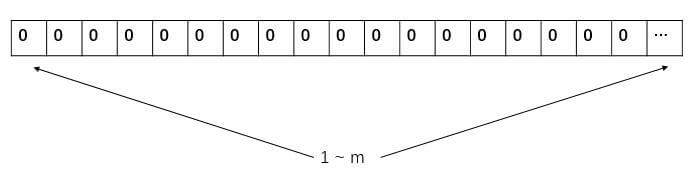
    step-1
  2. 使用 k 个相互独立的 Hash 函数，每个 Hash 函数将元素映射到 {1…m} 的范围内，并将对应的位置为 1。
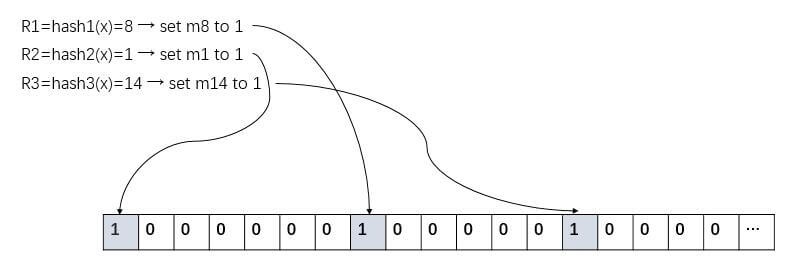
    step-2
    如上图所示，元素 x 分别被三个 Hash 函数映射到了三个位置 8、1、14，并将这三个位置从 0 变为 1。
  3. 若检查一个元素 y 是否存在，首先第一步使用 k 个 Hash 函数将元素 y 映射到 k 位。分别检测每一位是否为 0。若某一位为 0，则元素 y 一定不存在，若全部为 1，则有可能存在。

空间复杂度
BloomFilter 使用位向量来表示元素，而不存储本身，这样极大压缩了元素的存储空间。其空间复杂度为 O(m)，m 是位向量的长度。而 m 与插入总数量 n 的关系如公式 (1)(1) 所示

m=−nln⁡p(ln⁡2)2(1)m=-{\frac {n\ln p}{(\ln 2)^{2}}} \tag{1}

我们可以利用这个公式来算一下需要抓取 100 万个 URL 时 BloomFilter 所占据的空间。

假设要求误判率为 1%，因此该公式可转化为 m=9.6∗nm=9.6*n。故此时 BloomFilter 位向量的大小为 100w∗9.6=960wbit100w*9.6 = 960w bit，约 1.1M 内存空间。
只需要 1.1M 的内存空间，就可满足 100 万个 url 的去重需求，这个空间复杂度之低不可谓不惊人。
实际上，哪怕是 1 亿个 URL，也仅需 100M 左右的内存空间即可满足 BloomFilter 的空间需求，这对于绝大部分爬虫的体量来说，是完全可行的。

时间复杂度
时间复杂度方面 BloomFilter 的时间复杂度仅与 Hash 函数的个数 k 有关，即 O(k)O(k)

误判率

为什么说，在查找元素时，即使某个元素所映射的 k 位全部位 1，依然无法确定它一定存在？

这是因为当插入的元素很多的情况下，某个元素即使之前不存在，但是它所映射的 k 位已经被之前其他的元素置为 1 了，这样就会出现误判，BloomFilter 会认为它已经存在了。

但是这个概率是非常小的。根据维基百科的推导公式来说，误判率的大小 p 满足以下公式 (2)(2):

ln⁡p=−mn(ln⁡2)2(2)\ln p = -{\frac {m}{n}}\left(\ln 2\right)^{2} \tag{2}

其中 m 为位向量的长度，n 为要插入元素的总数。当误判率为 1% 时,mn=9.6\frac mn=9.6 即每个元素仅需要 9.6 个字节存储即可

Hash 函数的个数 k，与误判率大小 p 的关系为公式 (3)(3) 所示

k=−ln⁡pln⁡2(3)k = {-{\ln p} \over {\ln 2}} \tag{3}

当误判率大小为 0.1 时，k 为 3。当误判率大小为 0.01 时，k 为 7

而，k 与位向量的长度 m 和插入元素的总数 n 的关系为公式 (4)(4) 所示

k=mnln⁡2(4)k = {\frac {m}{n}}\ln 2 \tag{4}

缺点

删除元素

BloomFilter 由于并不存储元素，而是用位的 01 来表示元素是否存在，并且很有可能一个位时被多个元素同时使用。所以无法通过将某元素对应的位置为 0 来删除元素。

幸运的是，目前学术界和工业界都有很多方法扩展已解决以上问题。具体可以参考本文第三部分 [BloomFilter 的优化和扩展](#BloomFilter 的优化和扩展)

Guava’s BloomFilter 源码剖析

Guava 是 Google 主导开发的基于 Java 6 开发的一个开源工具包, 其中便包含了 一个 BloomFilter 的实现。Guava’s BloomFilter 也是一个完全可工程化的 BloomFilter 的最佳实现范本，本文基于 Guava 19.0 的源码进行解读。

使用介绍

在讲解 Guava BloomFilter 的源码之前，还是要用一个简单的例子来说明下 Guava 中 BloomFilter 的使用，以便更好地理解 Guava。具体代码在 这里

在这个例子中，我们定义了一个 Person 类, 来表示一个人的姓名信息。代码如下

class Person{
  private String firstName;
  private String lastName;
  //getter..
  //setter..
}

在这个例子中，我们会将 Person 对象传递给 BloomFilter，当该对象的 firstName+lastName 在 BloomFilter 中存在时，会提示已存在，不将其加入 BloomFilter 中。

但是对于 BloomFilter 来说，它无法主动地知道如何把一个自定义类的对象转化为 hash 值，也许有人会说，重写类的 hashcode 方法不就行了吗？

事实上还真不行，因为这和 BloomFilter 的概念冲突了，BloomFilter 简单来说是通过计算出 k 个不同的 hash 值来定位元素，重写了 hashcode 那么这个计算 k 个 hash 的过程将毫无意义。

Guava 通过将自定义对象分解为普通类型，对普通类型进行 Hash 值的计算，来将对象存入 BloomFilter 中。

这里 Guava 引入了一个叫做 Funnel 的类，Funnel 类定义了如何把一个具体的对象类型分解为原生字段值，从而将值分解为 Byte 以供后面 BloomFilter 进行 hash 运算。通过使用这个类，我们可以自己定义一个属于自己类的 Funnel。如下代码

enum PersonFunnel implements Funnel<Person> {
    INSTANCE;

    @Override
    public void funnel(Person person, PrimitiveSink into) {
        into.putString(person.getFirstName(), Charset.defaultCharset())
                .putString(person.getLastName(), Charset.defaultCharset());
    }
}

此外，Guava 预定义了一些原生类型的 Funnel，如 String、Long、Integer。具体代码可以在 这里看到。当我们的 BloomFilter 存储的是这些原生类型时，不用再额外自行写 Funnel，直接使用 Guava 预定义的这些即可。

以下是整个代码调用的流程

class BloomFilterSample{
  public static void main(String[] args) {
        // 创建一个 BloomFilter，其预计插入的个数为 10，误判率大约为 0.01
        BloomFilter<Person> bloomFilter = BloomFilter.create(PersonFunnel.INSTANCE, 10, 0.01);
        // 查询 new Person("chen", "yahui") 是否存在
        System.out.println(bloomFilter.mightContain(new Person("chen", "yahui"))); //false
        // 将 new Person("chen", "yahui") 对象放入 BloomFilter 中
        bloomFilter.put(new Person("chen","yahui"));
        // 再次查询 new Person("chen", "yahui") 是否存在
        System.out.println(bloomFilter.mightContain(new Person("chen", "yahui"))); //true
  }
}

源码解读

初始化 BloomFilter

在例子中，我们通过调用 BloomFilter.create 工厂方法来生成一个 BloomFilter

<T> BloomFilter<T> create(Funnel<? super T> funnel,
                          long expectedInsertions,  // 预期会插入多少元素
                          double fpp, // 自定义误判率
                          Strategy strategy //Hash 策略
                          ) {
    if (expectedInsertions == 0) {
      expectedInsertions = 1;
    }
    ...
    // 根据插入的数量和误判率来得出位向量应有的长度, 这里使用的算法就是公式 2
    long numBits = optimalNumOfBits(expectedInsertions, fpp);
    // 根据插入的数量和位向量的长度来得出应该用多少个 Hash 函数，这里使用的算法是公式 4
    int numHashFunctions = optimalNumOfHashFunctions(expectedInsertions, numBits);
    return new BloomFilter<T>(new BitArray(numBits), numHashFunctions, funnel, strategy);
}

整个创建流程非常清晰，如果看懂了本文的算法描述部分，应该不难理解该段代码。整个初始化流程的目的主要有两个：根据参数计算出位向量的长度以及 Hash 函数的个数

  1. 根据预期插入的数量 expectedInsertions 和自定义的误判率 fpp 来得到位向量的长度 numBits，其中 optimalNumOfBits 的实现如下
// 根据插入的数量和误判率来得出位向量应有的长度
static long optimalNumOfBits(long n, double p) {
    if (p == 0) {
      p = Double.MIN_VALUE;
    }
    return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}

可以很明显看出，optimalNumOfBits 的源码，其实就是对公式 (1)(1) 的实现
2. 根据插入的数量 expectedInsertions 和位向量的长度 numBits 来得出应该用多少个 Hash 函数，其中 optimalNumOfHashFunctions 的实现如下

static int optimalNumOfHashFunctions(long n, long m) {
    // (m / n) * log(2), but avoid truncation due to division!
    return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
  }

同样，optimalNumOfHashFunctions 也对应了我们算法中公式 (4)(4)
3. 根据 numBits 生成 BitArray。
BitArray 是 Guava 中位向量的表示，具体的实现细节，将会在下一节中讲述。

位向量的表示

本节主要讲述了 Guava 中位向量的表示，此部分对于 BloomFilter 的整体算法流程的理解关联性并不是特别强。读者如对此部分不感兴趣，可直接跳过此节。

位向量是 BloomFilter 的存储表示，所有的数据都在 BloomFilter 中存储。如何更高效地表示位向量也是一个优质的 BloomFilter 代码重要考量标准。
在 Guava 中，自定义了 BitArray 类, 代码如下：

class BitArray {
    final long[] data;
    long bitCount;

    BitArray(long bits) {
      // 对于长度为 m 的位向量来说，对应的 long 数组的长度应为 m/64 向上取整。
      this(new long[Ints.checkedCast(LongMath.divide(bits, 64, RoundingMode.CEILING))]);
    }

    boolean set(long index) {
        if (!get(index)) {
          data[(int) (index >>> 6)] |= (1L << index);
          bitCount++;
          return true;
        }
        return false;
    }

    boolean get(long index) {
      return (data[(int) (index >>> 6)] & (1L << index)) != 0;
    }
  }

在 BitArray 中，使用 long 数组来表示位向量，一个数组元素对应位向量的 64 位，所以对于长度为 m 的位向量来说，对应的 long 数组的长度应为 m/64 向上取整。
即

new long[Ints.checkedCast(LongMath.divide(bits, 64, RoundingMode.CEILING))]

在 BloomFilter 算法讲解部分，我们可以看到，对于位向量的常用操作主要有两个，将位向量某一位置为 1 以及查看位向量某一位是否为 1。分别对应源码中的 set 操作和 get 操作。
本文只讲下 get 方法的源码部分，set 方法与 get 方法类似，不再累述。

get 方法大致可以分为两部分

  1. data[(int) (index >>> 6)] 定位到元素
    上面讲到 long 数组的每一个元素都包含位向量其中的 64 位，如果想要找出某个位的 bit，那么首先第一步就是定位到该 bit 所在的元素编号。我们一般的做法是 index/64。
    而源码中使用了 index >>> 6, 逻辑右移 6 位，26=642^6=64, 其效果与除以 64 相同。采用位运算的速度比普通的除法要快很多。
  2. … & (1L << index) 获取位的状态
    源码中直接将要查看的 bit 以及同一数组元素块的 64 位 bits 一起取出，将 1L 左移 index 位后求且运算，最终即可得出该位的值。

k 个 hash 函数的选取

在 Hash 函数的选取方面，一个很重要的问题就是如何选取多个 Hash 函数？

我们在对元素进行映射的时候，Hash 函数的个数 k 的选取，最少也得为 3 个，最多可能多达十几个甚至更多，而目前世界上可商用的高质量的开源的 Hash 方法，远远达不到 BloomFilter 的需求。
在论文 《Bloom Filters in Probabilistic Verification》 中提出了一种算法，把原本需要几十个 hash 函数的 bloom filter 转化成了两个 hash 值的运算，完美地解决了这个问题。

gi(x)=h1(x)+ih2(x)+i2modm(5)g_i(x)=h_1(x)+ih_2(x)+i^2 mod m \tag{5}

上述公式中 gi(x)g_i(x) 为第 i 个 hash 函数。其中 0<i<k0 < i < k。也就是说使用 hash1() 和 hash2() 对一次输入求出两个不同的 hash 值，然后将这两个 hash 值代入公式，求出 k 个 hash 值。
整体的计算流程如下：

// 准备阶段
h1 = hash1(input), h2 = hash2(input)

// 求出 k 个 hash 值
g0(x) = h1                    第 0 个 hash 函数求出的 hash 值
g1(x) = h1+h2+1               第 1 个 hash 函数求出的 hash 值
g2(x) = h1+2*h2+4             第 2 个 hash 函数求出的 hash 值
...
gk-1(x) = h1+(k-1)*h2+(k-1)^2 第 k-1 个 hash 函数求出的 hash 值

在哈佛大学 2006 年的一篇论文《Less hashing, same performance: building a better bloom filter》中，对此方法的有效性进行了验证，证明了此种方法不会对 BloomFilter 的效率有所恶化。

Guava 实现了两种策略 MURMUR128_MITZ_32 和 MURMUR128_MITZ_64，其所有的实现类为 BloomFilterStrategies。
本文针对 Guava 的 BloomFilter 所采用的 MURMUR128_MITZ_32 策略进行讲解，

 public <T> boolean put(T object,
                        Funnel<? super T> funnel,
                        int numHashFunctions,
                        BitArray bits) {
      long bitSize = bits.bitSize();
      long hash64 = Hashing.murmur3_128().hashObject(object, funnel).asLong();
      int hash1 = (int) hash64;
      int hash2 = (int) (hash64 >>> 32);

      boolean bitsChanged = false;
      for (int i = 1; i <= numHashFunctions; i++) {
        int combinedHash = hash1 + (i * hash2);
        // Flip all the bits if it's negative (guaranteed positive number)
        if (combinedHash < 0) {
          combinedHash = ~combinedHash;
        }
        bitsChanged |= bits.set(combinedHash % bitSize);
      }
      return bitsChanged;
    }
}

MURMUR128_MITZ_32 是对公式 (5)(5) 的一个实现的体现。首先根据 MurMurHash 计算出某个对象的 64 位 hash 值，将其分为两段，后 32 位为 hash1，前 32 位为 hash2。
将 hash1 看成公式 (5)(5) 中的 h1(x) 计算后的结果，hash2 看做是 h2(x) 计算后的结果，同时省去公式中的 i2i^2，将 hash1 和 hash2 代入公式计算。

在 Hash 函数选取方面，Guava 采用了 MurmurHash3 算法。MurmurHash 算法是 2008 年提出的一种 Hash 算法，运算简单高效，而且随机性强。目前最新的版本为 MurmurHash3。

MurmurHash3 能够产生出 32-bit 或 128-bit 两种哈希值。在 MURMUR128_MITZ_32 和 MURMUR128_MITZ_64 都选择使用了 128-bit 的结果。二者不同的是，MURMUR128_MITZ_32 仅使用 128-bit 的前 64 位。而 MURMUR128_MITZ_64 完全使用了 128 位的结果。

BloomFilter 的优化和扩展

Counting BloomFilter

上文提到布隆过滤器无法支持元素的删除操作, Counting BloomFilter 通过存储位元素每一位的置为 1 的数量，使得布隆过滤器可以支持删除操作。
但是这样会数倍地增加布隆过滤器的存储空间。

参考